NSGA-II
NSGA-II is a fast, elitist multiobjective evolutionary algorithm designed to efficiently approximate the Pareto-optimal front. It overcomes several issues found in earlier nondominated sorting approaches by reducing computational complexity, ensuring elitism, and eliminating the need for a sharing parameter.
Key Features
-
Fast Nondominated Sorting: NSGA-II sorts the population based on Pareto dominance with a computational complexity of \(O(MN^2)\), where \(M\) is the number of objectives and \(N\) is the population size.
-
Elitist Selection: The algorithm creates a combined pool of parent and offspring populations. From this pool, the best solutions are chosen based on fitness and diversity. This elitist strategy ensures that the best-found solutions are preserved over generations.
-
Crowding Distance for Diversity Maintenance: To maintain a diverse Pareto front, NSGA-II computes a crowding distance for each individual. For each front, the crowding distance \(d_i\) of an individual \(i\) is calculated as:
$$ d_i = \sum_{m=1}^{M} \frac{f_{m}^{(i+1)} - f_{m}^{(i-1)}}{f_{m}^{\max} - f_{m}^{\min}}, $$
where:
- \(f_{m}^{(i)}\) is the value of the \(m\)-th objective for the \(i\)-th individual (after sorting the individuals according to that objective),
- \(f_{m}^{\max}\) and \(f_{m}^{\min}\) are the maximum and minimum values of the \(m\)-th objective in that front, respectively.
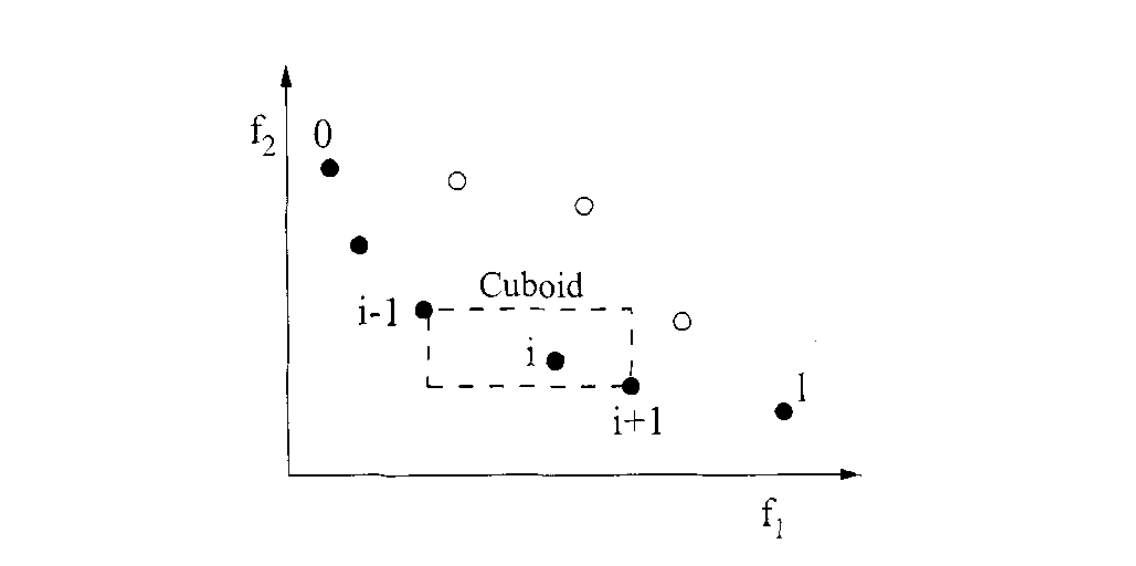
Individuals with a larger crowding distance are in less crowded regions and are preferred when selecting among solutions with the same non-domination rank, thereby promoting diversity across the Pareto front.
- Constraint Handling: When constraints_fn are present, NSGA-II modifies the selection process:
- Feasible Solutions First: Feasible individuals (those satisfying all constraints_fn) are always preferred over infeasible ones.
- Ranking: Among feasible solutions, those with a better (i.e., lower) nondominated rank are favored.
- Crowding Distance: Finally, if individuals share the same rank, the one with a larger crowding distance is selected. This ensures that, within the same rank, solutions from less crowded regions of the objective space are chosen.
ZDT3 Problem
ZDT3 is a widely used benchmark in multiobjective optimization, especially for testing evolutionary algorithms. It challenges algorithms with:
- Two Conflicting Objectives:
- \(f_1(\mathbf{x}) = x_1\)
-
\(f_2(\mathbf{x}) = g(\mathbf{x}) \cdot h(f_1(\mathbf{x}), g(\mathbf{x}))\)
-
Auxiliary Functions:
- \(g(\mathbf{x}) = 1 + \frac{9}{n-1}\sum_{i=2}^{n} x_i\)
-
\(h(f_1, g) = 1 - \sqrt{\frac{f_1}{g}} - \frac{f_1}{g}\sin(10\pi f_1)\)
-
Key Characteristics:
- Discontinuous Pareto Front: The optimal solutions are spread over several disconnected segments.
- Nonconvexity: The Pareto front is nonconvex, making convergence more challenging.
- Diversity Maintenance: The discontinuities force algorithms to preserve a diverse set of solutions.
Domain: Each decision variable \(x_i\) typically belongs to the interval \([0, 1]\), and the problem is often considered with \(n = 30\) variables.
ZDT3 is ideal for evaluating how well an algorithm can balance convergence toward the Pareto-optimal front while maintaining diversity in the presence of a complex, discontinuous solution landscape.
:dep ndarray = "*"
:dep moors = "*"
:dep plotters = "0.3.6"
use ndarray::{Array2, Axis, Ix2, s};
use moors::{
impl_constraints_fn,
algorithms::Nsga2Builder,
duplicates::CloseDuplicatesCleaner,
operators::{GaussianMutation, RandomSamplingFloat, ExponentialCrossover},
genetic::Population
};
use plotters::prelude::*;
/// Evaluate the ZDT3 objectives in a fully vectorized manner.
fn evaluate_zdt3(genes: &Array2<f64>) -> Array2<f64> {
// First objective: f1 is simply the first column.
// NOTE: We clamp to [0,1] during evaluation to keep the domain consistent with ZDT3.
// This mirrors the Python setup where variables are constrained to [0,1].
let n = genes.nrows();
let m = genes.ncols();
let clamped = genes.mapv(|v| v.clamp(0.0, 1.0));
let f1 = clamped.column(0).to_owned();
// Compute g for each candidate: g = 1 + (9/(n-1)) * sum(x[1:])
let tail = clamped.slice(s![.., 1..]);
let sums = tail.sum_axis(Axis(1));
let g = sums.mapv(|s| 1.0 + (9.0 / ((m as f64) - 1.0)) * s);
// Compute h for each candidate: h = 1 - sqrt(f1/g) - (f1/g)*sin(10*pi*f1)
let ratio = &f1 / &g;
let sin_term = f1.mapv(|v| (10.0 * std::f64::consts::PI * v).sin());
let h = 1.0 - ratio.mapv(|r| r.sqrt()) - &(&ratio * &sin_term);
// Compute the second objective: f2 = g * h
let f2 = &g * &h;
let mut result = Array2::<f64>::zeros((n, 2));
result.column_mut(0).assign(&f1);
result.column_mut(1).assign(&f2);
result
}
// Create constraints using the macro impl_constraints_fn
impl_constraints_fn!(BoundConstraints, lower_bound = 0.0, upper_bound = 1.0);
/// Compute the theoretical Pareto front for ZDT3.
///
/// Returns:
/// f1_theo (np.ndarray): f1 values on the theoretical front.
/// f2_theo (np.ndarray): Corresponding f2 values.
///
/// Instead of using a dense linspace, we sample only a few points per interval to
/// clearly illustrate the discontinuous nature of the front.
fn zdt3_theoretical_front() -> (Vec<f64>, Vec<f64>) {
// Define the intervals for f1 where the Pareto front exists
let intervals: &[(f64, f64)] = &[
(0.0, 0.0830015349),
(0.1822287280, 0.2577623634),
(0.4093136748, 0.4538828821),
(0.6183967944, 0.6525117038),
(0.8233317983, 0.85518),
];
let mut f1_theo: Vec<f64> = Vec::new();
let mut f2_theo: Vec<f64> = Vec::new();
// Use a small number of points per interval (e.g., 20) to highlight the discontinuities.
for (start, end) in intervals.iter().copied() {
let steps = 20usize;
for i in 0..steps {
let t = i as f64 / (steps as f64 - 1.0);
let f1 = start + t * (end - start);
let f2 = 1.0 - f1.sqrt() - f1 * (10.0 * std::f64::consts::PI * f1).sin();
f1_theo.push(f1);
f2_theo.push(f2);
}
}
(f1_theo, f2_theo)
}
// Set up the NSGA2 algorithm with the above definitions
let population: Population<Ix2, Ix2> = {
let mut algorithm = Nsga2Builder::default()
.sampler(RandomSamplingFloat::new(0.0, 1.0))
.crossover(ExponentialCrossover::new(0.75))
.mutation(GaussianMutation::new(0.1, 0.01))
.duplicates_cleaner(CloseDuplicatesCleaner::new(1e-5))
.fitness_fn(evaluate_zdt3)
.constraints_fn(BoundConstraints)
.num_vars(30)
.population_size(200)
.num_offsprings(200)
.num_iterations(300)
.mutation_rate(0.1)
.crossover_rate(0.9)
.keep_infeasible(false)
.verbose(false)
.seed(42)
.build()
.expect("Failed to build NSGA2");
// Run the algorithm
algorithm.run().expect("NSGA2 run failed");
algorithm.population.unwrap().clone()
};
// Get the best Pareto front obtained (as a Population instance)
let fitness = population.fitness;
// Extract the obtained fitness values (each row is [f1, f2])
let f1_found: Vec<f64> = fitness.column(0).to_vec();
let f2_found: Vec<f64> = fitness.column(1).to_vec();
// Compute the theoretical Pareto front for ZDT3
let (f1_theo, f2_theo) = zdt3_theoretical_front();
// Plot the theoretical Pareto front and the obtained front
let mut svg = String::new();
{
let backend = SVGBackend::with_string(&mut svg, (1000, 700));
let root = backend.into_drawing_area();
root.fill(&WHITE).unwrap();
// Compute min/max from actual data
let (mut x_min, mut x_max) = (f1_theo[0], f1_theo[0]);
let (mut y_min, mut y_max) = (f2_theo[0], f2_theo[0]);
for &x in f1_theo.iter().chain(f1_found.iter()) {
if x < x_min { x_min = x; }
if x > x_max { x_max = x; }
}
for &y in f2_theo.iter().chain(f2_found.iter()) {
if y < y_min { y_min = y; }
if y > y_max { y_max = y; }
}
// Add a small margin (5%)
let xr = (x_max - x_min);
let yr = (y_max - y_min);
x_min -= xr * 0.05;
x_max += xr * 0.05;
y_min -= yr * 0.05;
y_max += yr * 0.05;
let mut chart = ChartBuilder::on(&root)
.caption("ZDT3 Pareto Front: Theoretical vs Obtained", ("DejaVu Sans", 22))
.margin(10)
.x_label_area_size(40)
.y_label_area_size(60)
.build_cartesian_2d(x_min..x_max, y_min..y_max)
.unwrap();
chart.configure_mesh()
.x_desc("f1")
.y_desc("f2")
.axis_desc_style(("DejaVu Sans", 14))
.light_line_style(&RGBColor(220, 220, 220))
.draw()
.unwrap();
// Plot theoretical front as markers (e.g., diamonds) to show discontinuities.
chart.draw_series(
f1_theo.iter().zip(f2_theo.iter()).map(|(&x, &y)| {
Circle::new((x, y), 5, RGBColor(31, 119, 180).filled())
})
).unwrap()
.label("Theoretical Pareto Front")
.legend(|(x, y)| Circle::new((x, y), 5, RGBColor(31, 119, 180).filled()));
// Plot obtained front as red circles.
chart.draw_series(
f1_found.iter().zip(f2_found.iter()).map(|(&x, &y)| {
Circle::new((x, y), 3, RGBColor(255, 0, 0).filled())
})
).unwrap()
.label("Obtained Front")
.legend(|(x, y)| Circle::new((x, y), 3, RGBColor(255, 0, 0).filled()));
chart.configure_series_labels()
.border_style(&RGBAColor(0, 0, 0, 0.3))
.background_style(&WHITE.mix(0.9))
.label_font(("DejaVu Sans", 13))
.draw()
.unwrap();
root.present().unwrap();
}
// Emit as rich output for evcxr
println!("EVCXR_BEGIN_CONTENT image/svg+xml\n{}\nEVCXR_END_CONTENT", svg);
import numpy as np
import matplotlib.pyplot as plt
from pymoors import (
Nsga2,
RandomSamplingFloat,
GaussianMutation,
ExponentialCrossover,
CloseDuplicatesCleaner,
Constraints
)
from pymoors.schemas import Population
from pymoors.typing import TwoDArray
np.seterr(invalid="ignore")
def evaluate_zdt3(population: TwoDArray) -> TwoDArray:
"""
Evaluate the ZDT3 objectives in a fully vectorized manner.
"""
# First objective: f1 is simply the first column.
f1 = population[:, 0]
n = population.shape[1]
# Compute g for each candidate: g = 1 + (9/(n-1)) * sum(x[1:])
g = 1 + (9 / (n - 1)) * np.sum(population[:, 1:], axis=1)
# Compute h for each candidate: h = 1 - sqrt(f1/g) - (f1/g)*sin(10*pi*f1)
h = 1 - np.sqrt(f1 / g) - (f1 / g) * np.sin(10 * np.pi * f1)
# Compute the second objective: f2 = g * h
f2 = g * h
return np.column_stack((f1, f2))
def zdt3_theoretical_front():
"""
Compute the theoretical Pareto front for ZDT3.
Returns:
f1_theo (np.ndarray): f1 values on the theoretical front.
f2_theo (np.ndarray): Corresponding f2 values.
Instead of using a dense linspace, we sample only a few points per interval to
clearly illustrate the discontinuous nature of the front.
"""
# Define the intervals for f1 where the Pareto front exists
intervals = [
(0.0, 0.0830015349),
(0.1822287280, 0.2577623634),
(0.4093136748, 0.4538828821),
(0.6183967944, 0.6525117038),
(0.8233317983, 0.85518),
]
f1_theo = np.array([])
f2_theo = np.array([])
# Use a small number of points per interval (e.g., 20) to highlight the discontinuities.
for start, end in intervals:
f1_vals = np.linspace(start, end, 20)
f2_vals = 1 - np.sqrt(f1_vals) - f1_vals * np.sin(10 * np.pi * f1_vals)
f1_theo = np.concatenate((f1_theo, f1_vals))
f2_theo = np.concatenate((f2_theo, f2_vals))
return f1_theo, f2_theo
# Set up the NSGA2 algorithm with the above definitions
algorithm = Nsga2(
sampler=RandomSamplingFloat(min=0, max=1),
crossover=ExponentialCrossover(exponential_crossover_rate=0.75),
mutation=GaussianMutation(gene_mutation_rate=0.1, sigma=0.01),
fitness_fn=evaluate_zdt3,
constraints_fn=Constraints(lower_bound=0.0, upper_bound=1.0),
duplicates_cleaner=CloseDuplicatesCleaner(epsilon=1e-5),
num_vars=30,
population_size=200,
num_offsprings=200,
num_iterations=300,
mutation_rate=0.1,
crossover_rate=0.9,
keep_infeasible=False,
verbose=False,
)
# Run the algorithm
algorithm.run()
# Get the best Pareto front obtained (as a Population instance)
best: Population = algorithm.population.best_as_population
# Extract the obtained fitness values (each row is [f1, f2])
obtained_fitness = best.fitness
f1_found = obtained_fitness[:, 0]
f2_found = obtained_fitness[:, 1]
# Compute the theoretical Pareto front for ZDT3
f1_theo, f2_theo = zdt3_theoretical_front()
# Plot the theoretical Pareto front and the obtained front
plt.figure(figsize=(10, 6))
# Plot theoretical front as markers (e.g., diamonds) to show discontinuities.
plt.scatter(
f1_theo, f2_theo, marker="D", color="blue", label="Theoretical Pareto Front"
)
# Plot obtained front as red circles.
plt.scatter(f1_found, f2_found, c="r", marker="o", s=10, label="Obtained Front")
plt.xlabel("$f_1$", fontsize=14)
plt.ylabel("$f_2$", fontsize=14)
plt.title("ZDT3 Pareto Front: Theoretical vs Obtained", fontsize=16)
plt.legend()
plt.grid(True)
